Newton a-t-il dérivé l’accélération de Coriolis ?

L’édition de 1905 de la revue scientifique allemande Annalen der Physik est devenue célèbre pour les cinq articles révolutionnaires d’Albert Einstein, qui ouvriront la voie vers la « physique moderne ». Ce qui est moins connu est que cette même édition d’Annalen fut aussi le lieu d’un vif débat entre trois scientifiques d’Europe centrale[1] sur l’interprétation correcte de l’effet Coriolis. Les trois scientifiques n’arrivant pas à se mettre d’accord, le rédacteur en chef Max Planck leur demanda de poursuivre leur discussion ailleurs[2].

Aujourd’hui, nous sommes fiers de notre bonne connaissance de la mécanique quantique et de la théorie de la relativité – mais l’effet Coriolis continue de nous laisser perplexes ! Ainsi n’est-il pas surprenant qu’Alexandre Moatti ait intitulé sa biographie de Gaspard-Gustave Coriolis (1794-1843) Le Mystère Coriolis[3].

 

1. Le mémoire de Coriolis de 1835

Lors des années 1830, au moment où la Révolution industrielle battait son plein, Coriolis commença à s’intéresser à la dynamique des machines à pièces tournantes. Dans quelle mesure la force centrifuge, et donc la tension s’exerçant sur la machine, change-t-elle lorsqu’une pièce de la machine est aussi en mouvement par rapport à la rotation ?

Dans son mémoire de 1835, Coriolis montra que dans une machine qui tourne à une vitesse angulaire Ω où une pièce est en mouvement par rapport à la rotation à la vitesse V_r, une force supplémentaire 2ΩV_r doit s’ajouter à la force centrifuge ordinaire Ω²R ou U²/R (où R est la distance vis-à-vis de l’axe de rotation et U la vitesse de rotation). Cette force supplémentaire, qui sera connue bien ultérieurement sous le nom de « force de Coriolis », est indépendante de R et perpendiculaire au mouvement relatif V_r. Dans une rotation anti-horaire, elle est dirigée vers la droite (et vers la gauche dans une rotation horaire). Puisque le mouvement est dévié à angle droit, elle ne peut que changer de direction ; sa vitesse (l’énergie cinétique) ne change pas. Coriolis nomme cette force complémentaire la force centrifuge composée.

Dans cet article, on postulera que les difficultés rencontrées depuis 180 ans pour comprendre cette « force de Coriolis » découlent non seulement de démarches erronées – qui ont tendance à l’isoler d’un point de vue conceptuel, sans prendre en compte la force centrifuge –, mais aussi de tentatives de la visualiser au sein d’un référentiel relatif. Et c’est là que certaines idées des Principia d’Isaac Newton peuvent venir à la rescousse.

 

2. Représenter des forces fictives

Dans la dérivation vectorielle standard (accélération relative dans un système de rotation Ω, d’un mouvement relatif V_r à une distance R), les deux forces sont liées de manière organique :

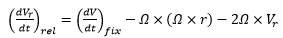            (1)

Même si la structure mathématique du terme de Coriolis 2Ω× V_r semble être différente de celle du terme centrifuge Ω×(Ω×R), physiquement les deux forces ont la même nature centrifuge[4].

1. 1 Une représentation erronée de la force centrifuge

Une autre source de confusion est notre tendance à visualiser incorrectement les forces fictives – non seulement la force de Coriolis, mais également la force centrifuge. En effet, cette dernière est couramment représentée par le biais d’une image contenant les paramètres pertinents : la vitesse de rotation U, la distance vis-à-vis du centre de rotation R et la rotation Ω (antihoraire ici). Cette image pourrait ressembler à celle figurant ci-dessous, où la force centrifuge se dirige vers l’extérieur le long d’une ligne passant par le centre de rotation (figure 1).

 

Figure 1 : Une image courante de la relation entre un objet suivant un mouvement curviligne (U) et la force centrifuge (C_e) à une distance R du centre de rotation Ω. L’image est barrée car elle induit en erreur et n’est pas tout à fait exacte.

 

Mais ce faisant nous mélangeons deux référentiels différents. La trajectoire du mouvement est représentée dans un référentiel absolu, comme vue de l’extérieur. Or, la force centrifuge ne peut se ressentir que de l’« intérieur » et ne peut se représenter que dans un référentiel relatif.

Et pourtant, l’image s’accorde avec le « bon sens » car, lorsque nous faisons un tour de manège ou que nous sommes assis dans un bus qui prend un virage, nos yeux peuvent estimer visuellement la courbure. Les forces que nous ressentons sont « à l’intérieur » du manège ou du bus, mais nos yeux se dirigent vers l’« extérieur ».

 

2.2. Une représentation juste mais inintéressante de la force centrifuge

Mais imaginons que nous ayons les yeux bandés – ou que nous voyagions la nuit dans un train dernier cri qui avance sans heurts. Dans ce cas, il est quasiment impossible de connaître la direction du train (en arrière ou en avant ?). Lorsque le train prend un virage, on ne s’en aperçoit que parce que la force centrifuge nous pousse dans une certaine direction, et si l’on est assis correctement notre siège fournit une force centripète se dirigeant dans le sens inverse, ce qui nous maintient en place. Notre expérience sensorielle du trajet peut donc se résumer ainsi :

 

Figure 2 : Le même mouvement que celui indiqué dans la Figure 1, mais maintenant représenté seulement dans un référentiel relatif, suivant l’objet en mouvement, et non dans un référentiel absolu, où il est observé de l’extérieur de l’objet.

 

Cette image, quoique juste d’un point de vue physique, pourrait paraître assez fade ou inintéressante. Ainsi, elle ne fournit aucune information quant à la courbure du mouvement ou si celui-ci se fait en avant ou en arrière.

 

2.3 Une représentation erronée de la force de Coriolis

Si malgré cela on persiste à vouloir une image « saisissable » quoique toujours erronée de la déviation de Coriolis, elle pourrait ressembler à ceci (Figure 3):

 

Figure 3 : Une image de la force de Coriolis en tant qu’un des deux composants d’une force centrifuge décomposée. L’image est facile à comprendre mais trompeuse.

 

Avec un mouvement vers l’intérieur V_r, la trajectoire de son mouvement absolu ne suit plus exactement la rotation mais se tourne radialement en spirale vers l’intérieur, vers le centre de rotation. L’action centrifuge, qui est perpendiculaire à la trajectoire, ne se dirige plus le long d’une ligne qui passe par le centre de rotation.

On décompose le vecteur C_e en deux vecteurs. L’un passe directement par le centre de rotation ; il s’agit de la force centrifuge « ordinaire » Ω²R. L’autre, perpendiculaire, est la « force centrifuge composée » 2ΩV_r de Coriolis. Puisque le mouvement relatif V_r se fait radialement vers l’intérieur, on voit également que cette force de Coriolis se dirige vers la droite du mouvement relatif pour la rotation antihoraire (comme celle de la Terre).

On se trouve donc face à une contradiction : d’un côté, une image « compréhensible » mais incorrecte ; de l’autre côté, une image juste mais qui ne semble pas correspondre à ce que nous dit le « bon sens ». Mais il existe une solution, qui consiste à abandonner les référentiels relatifs pour n’utiliser que des référentiels absolus.

 

3. Représentation de forces dans un référentiel absolu

Selon une convention internationale assez étrange, l’« accélération de Coriolis » ne correspond pas à la force de Coriolis par unité de masse, mais à une accélération liée à l’accélération centripète, due à une force réelle, braquée dans le sens inverse de la force de Coriolis – tout comme la force centripète se dirige dans le sens inverse de la force centrifuge !

Pour commencer par cette dernière, il s’agit de l’action d’une force centrale U²/R se dirigeant vers l’intérieur (Figure 4).

 

Figure 4 : Une force centripète constante de magnitude Ω²R fait tourner un objet en un mouvement circulaire. Au lieu d’une force centrifuge se dirigeant vers l’extérieur en raison du mouvement courbe, nous avons un mouvement courbe dû à une force centripète se dirigeant vers l’intérieur. 

 

La trajectoire en spirale vers l’intérieur, due à une vitesse tangentielle U et une vitesse radiale V, peut désormais être considérée comme le résultat d’une force centripète se dirigeant vers l’intérieur, qui peut se décomposer en une force centripète ordinaire dirigée vers le centre de rotation et une force perpendiculaire, désormais orientée vers la gauche du mouvement radial relatif, l’accélération de Coriolis (figure 5).

 

Figure 5 : Afin que le corps se déplaçant de manière tangentielle se dirige radialement vers l’intérieur, une accélération centripète doit être appliquée, qui est la somme de l’accélération centripète ordinaire et l’accélération de Coriolis.

 

On peut aussi dire que l’accélération de Coriolis doit être appliquée sur un objet en mouvement afin d’éviter que celui-ci soit dévié par la force de Coriolis.

Il pourrait paraître étonnant de vouloir comprendre le mécanisme de déviation de Coriolis par l’étude de l’accélération de Coriolis vu d’un référentiel absolu, mais nous avons un puissant allié dans cette démarche : Sir Isaac Newton, auteur des Principia !

 

4. L’usage de la géométrie dans les Principia de Newton

Mondialement connus, les Principia sont disponibles en traduction dans la plupart des langues. Et pourtant, peu d’entre nous ont lu cet ouvrage voire même l’ont ouvert. C’est dommage, car même en feuilletant les pages on se rend compte de quelque chose d’étonnant : il n’y a pas d’équations algébriques, il n’y a que de la géométrie euclidienne. Newton pensait qu’en utilisant la géométrie euclidienne ses résultats seraient plus simples à comprendre, du moins en son temps (figure 6).

 

Figure 6 : Une planche tirée de l’édition française des Principia indiquant toutes les figures dans la Partie I. La « Fig.13 », au milieu, est celle qui nous intéressera ici.

 

Donnons un exemple de l’approche euclidienne de Newton, lié au problème du calcul de la force centripète. Cet exemple illustre également la beauté mathématique de son raisonnement.

 

Figure 6bis : Une page des Principia, indiquant la construction géométrique utilisée par Isaac Newton pour démontrer la deuxième loi de Kepler, qui correspond à la conservation du moment angulaire.

 

 

Figure 6ter : Avant de publier les Principia, Newton écrivit un texte plus court intitulé « De motu corporum in gyrum », dans lequel il a testé certaines de ses idées.

 

 

5. Appliquer la méthode de Newton

Supposons qu’un corps se déplace sans frottement de manière rectilinéaire de A à C en passant par B, au milieu de A et C (Figure 7).

 

Figure 7 : Un corps se déplace de manière rectilinéaire, sans frottement, de A à B (a), puis de B à C (b). En ce qui concerne les distances, AB = Bc ; on utilise les notations de Newton.

 

Au début des Principia, Newton montre que le rayon vecteur d’un corps qui se déplace de manière rectilinéaire par inertie et pendant des temps égaux couvre des aires égales et obéit donc à la deuxième loi de Kepler (figure 8).

 

 

Figure 8 : Le rayon vecteur du mouvement du corps par rapport au point S couvre des aires égales (verte et jaune) pendant des temps égaux, conformément à la deuxième loi de Kepler.

 

Newton supposait qu’au point B le corps subissait une force d’impulsion qui, si elle était seule, déplacerait le corps dans une nouvelle direction (flèche rouge, figure 9a). Mais, compte tenu du mouvement originel, le corps se déplacera selon une combinaison des deux directions (figure 9b).

 

Figure 9 (a) et (b) : Une force d’impulsion pousse le corps en B dans la direction de V (a). Le mouvement résultant vers C est une combinaison des mouvements de B à V et de B à c (b).

Dans la figure 8 nous avons vu que les triangles vert et jaune ont des aires égales. Mais qu’en est-il du nouveau triangle SBC, à traits rouges, dans la Figure 10 ?

 

 

Figure 10 : Il s’avére que l’aire BSC couverte par le rayon vecteur au regard de S (ligne rouge pointillée) a la même aire que l’aire jaune BSc couverte par le rayon vecteur au regard de S.

 

Newton montra que, comme les deux ont la même base SB et la même hauteur CC’ (égale à cc’), leurs aires sont égales (figure 11).

 

Figure 11 : La preuve de Newton que les aires BSC = BSc.

 

Quoique le mouvement du corps ait été dévié de la ligne droite vers une courbe, il vérifie néanmoins la deuxième loi de Kepler car son rayon vecteur au regard de S couvre des aires égales pendant des temps égaux (figure 12).

 

Figure 12 : Les rayons vecteurs du corps qui se déplace de A à C couvrent des aires égales pendant des temps égaux, selon la deuxième loi de Kepler.

 

Newton a ensuite appliqué ce même raisonnement aux intervalles de temps successifs : à chaque point C, D, E et F le corps est mu par une force d’impulsion dirigée vers le même point central C (figure 13).

 

Figure 13 : Figure 12, insérée dans son contexte dans les Principia de Newton.

 

Pendant le xvii^e et une grande partie du xviii^e siècle on pensait que la deuxième loi de Kepler, également connue sous le nom de la « loi des aires », ne s’appliquait qu’aux objets célestes (planètes, lunes, comètes, etc.). Mais déjà dans les Principia, Newton montra que les mêmes lois du mouvement qui guident les objets célestes sont valables sur Terre – parmi lesquelles la « loi des aires », qu’on appelle aujourd’hui la « conservation du moment angulaire ».

 

6. Newton et la force centripète

Mais Newton s’intéressait au calcul de la force centripète bien avant qu’il eût l’idée de dériver la deuxième loi de Kepler. Huygens avait exprimé la force centrifuge dès 1659 et les premières tentatives de Newton datent d’avant 1669 (il était âgé de 27 ans).

Il est fascinant de voir comment il utilise la proposition 36 – peu connue – du Livre III des Éléments d’Euclide. Dans cette proposition, Euclide montre qu’un rectangle construit avec le diamètre CE et la distance courte CD a la même aire que le carré défini par la longueur BC (Figure 14).

Ainsi, CE × CD = (BC)². Pour nos fins ici on l’applique à des symboles plus pertinents dans la Figure 14b) :

                                                               

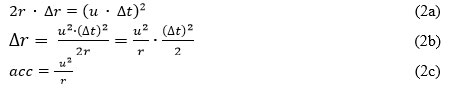
qui est l’équation pour la force centripète (par unité de masse).

 

Figure 14 (a) et (b) : Comment Isaac Newton a dérivé la force centripète de la Proposition 36 du Livre III d’Euclide, avec à gauche les notations de Newton (a) et à droite les notations applicables à notre étude (b).

 

Les Principia étaient peut-être assez faciles à lire il y a 300 ans, mais pour le lecteur moderne leur langage géométrique n’est guère compréhensible au premier abord. D’un autre côté, tout effort se voit justement récompensé par ces belles preuves utilisant Euclide.

 

7. Quelques dérivations de Coriolis à la Newton

En s’inspirant de Newton, nous appliquerons cette approche géométrique afin de dériver l’accélération centripète et l’accélération de Coriolis pour des mouvements tangentiels et radiaux, dans un référentiel absolu.

1. 1 Mouvement tangentiel

Nous dérivons d’abord une expression pour la force centripète en utilisant plus ou moins la même approche que Newton dans son texte daté d’avant 1669 (figure 15).

 

 

Figure 15 : Une dérivation géométrique de la force centripète.

 

Un corps se déplace avec une rotation Ω à une distance constante r du centre de rotation O. Une accélération centripète a dirigée vers l’intérieur fait dévier le corps par une distance vers l’intérieur Δs pendant une durée Δt. Sans cette force dirigée vers l’intérieur, l’objet se déplacerait de manière rectilinéaire de A à B par l’inertie Ω·r·Δt. En appliquant le théorème de Pythagore au triangle ABO, nous avons (Ω·r·Δt)² + r² = (Δs + r)², ce qui donne, en omettant les termes de deuxième ordre, Δs  = (Ω·r·Δt)²/2r = a·(Δt)²/2, ce qui à son tour donne pour résultat  a = Ω²r, l’accélération centripète.

Au mouvement tangentiel ΩR s’ajoute désormais la vitesse tangentielle u (figure 16).

 

Figure 16 : Dérivation de la force centripète (par unité de masse) pour un corps se déplaçant relativement de manière tangentielle à une vitesse différente de la vitesse de rotation (voir test pour plus de détails).

 

La force centripète est comme indiquée ci-dessus : le mouvement tangentiel u est ajouté à Ω·r

((Ω·r + u)Δt)² + r² = (Δs₁ + r)²                    (3a),

ce qui donne, en omettant les termes quadratiques :

(u·Δt)² + 2u.r.Ω·Δt² + (Ω·r·Δt)² = 2 Δs₁·r           (3b)

Δs₁ = (Ω²·r + 2Ω·u + u²/r) Δt²/2                    (3c)

c’est-à-dire, l’accélération centripète Ω²·r, l’accélération de Coriolis 2Ω·u et un soi-disant « terme d’accélération métrique » u²/r. Ce terme apparaît dans la plus simple des dérivations de la force de Coriolis (voir ci-dessous). Retournons brièvement au référentiel relatif, où existent des forces centrifuges.

 

7.2 Les termes « métriques »

La force centrifuge (par unité de masse) (C_e) qui s’exerce sur un objet à une distance R du centre de rotation est C_e = U²/R, où U = ΩR est la vitesse de rotation tangentielle. Dans le cas d’un mouvement tangentiel relatif u_r, la force centrifuge totale devient

       

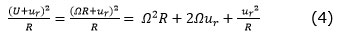
où le premier terme est la force centrifuge ordinaire Ω²R et le deuxième terme la force de Coriolis 2Ωu_r. On explique souvent le dernier terme métrique u_r²/R comme étant lié au système de coordonnées choisi[5]. Pour des vitesses usuelles, il est toujours inférieur au terme de Coriolis. Ils sont égaux lorsque

                                

où U est la vitesse de rotation correspondant à ΩR.

Dans les sciences géophysiques, où R fait référence au rayon de la Terre, le terme métrique n’est souvent pas pris en compte car u_r²/R  2Ω·u_r  lorsque u_r ne dépasse pas 100 m/s. Mais cet argument mathématique et numérique ne rend pas compte de la raison physique pour laquelle il est possible de ne pas prendre en compte le terme métrique dans beaucoup d’applications pratiques. Même s’il ne contient pas Ω et n’est donc pas lié à la rotation, il n’est pas pour autant vide de sens physique. Nous pouvons noter sa « nature centrifuge », c’est-à-dire une vitesse au carré divisée par une distance. Ceci nous rappelle que les forces centrifuges n’apparaissent pas seulement avec la rotation, mais avec n’importe quel mouvement courbe.

 

Figure 17 (a) et (b) : Mouvement relatif libre v_r sur une plateforme qui tourne (a) et mouvement courbe contraint v sur une plateforme qui ne tourne pas (b).

 

Dans la figure 17a) (à gauche), un corps se déplace librement sur une plateforme qui tourne (par exemple, un manège) et est affecté par une force centrifuge de Ω²R = 2 m/s² et une force de Coriolis 2Ωv_r = 2 m/s². Dans la figure 17b), la plateforme est immobile mais le mouvement du corps est contraint, comme ce fut le cas dans l’équation 2 ci-dessus, peut-être par la présence d’un rail (par exemple, un train jouet pour enfants). Ici la force centrifuge n’est pas due à une rotation mais au mouvement courbe.

 

1. 3 Les termes métriques en géophysique

La logique physique qui sous-tend l’abandon des termes métriques n’est pas le fait que u_r²/R  2Ω·u_r  mais le fait que les mouvements des courants océaniques et des vents atmosphériques ne sont pas contraints. Pourtant, un TGV voyageant entre Rennes et Paris est contraint à suivre les rails et est soumis à une accélération latérale due à la fois au terme de Coriolis et au terme métrique (fig. 18).

 

 

Figure 18 : Un TGV qui roule sur un rail droit de Rennes à Paris à une latitude de 47-48°. À une vitesse de u_r = 90 m/s et à une distance de 4 262 kilomètres de l’axe de rotation de la Terre, il est touché par deux accélérations vers le sud, qui ensemble font 8,2 mm/s². L’une est due à l’effet de Coriolis (6,79 mm/s²) et l’autre est due à la courbure de la latitude (1,43 mm/s²). Cette dernière accélération, qui est toujours dirigée vers l’équateur[6], existerait également si la Terre ne tournait pas. Si le train roulait dans le sens inverse, d’est en ouest, la force de Coriolis 2Ωsin(latitude)u_r par unité de masse serait dirigée dans le sens inverse, vers le nord, l’autre restant dirigée vers le sud : l’accélération totale, désormais dirigée vers le nord, serait 5,36 mm/s².

 

Un palet de hockey qui glisse sans frottement sur une couche de glace ne semble pas être un mouvement contraint, mais, comme la plupart des corps sur Terre, il est contraint – par la gravité et par la force de réaction de la surface solide – à rester sur la surface de la Terre. Avançant d’une vitesse V_r, il sera sujet partout sur Terre à une accélération verticale vers le haut

      

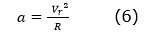
ce qui, en s’ajoutant à l’effet de Coriolis vertical, explique le dit « effet Eötvös », qui fait que les corps se déplaçant vers l’est sont plus légers et les corps déplaçant vers l’ouest sont plus lourds[7]. Les géodésistes doivent prendre en compte ce fait lorsqu’ils mesurent la gravité de la Terre à partir d’une plateforme mobile. Retournons maintenant à la « force de Coriolis » et aux accélérations, vues à partir d’un référentiel absolu.

7.4 Le mouvement radial

Prenons un corps qui se déplace avec une rotation Ω de A à C, et qui se dirige aussi radialement vers l’intérieur, vers G, à une vitesse v, couvrant la distance Δr = v·Δt. (Figure 19).

 

 

Figure 19 : Un corps se déplaçant radialement de A prend part à la rotation tout en se déplaçant radialement vers l’intérieur, ce qui fait qu’il arrive à G au lieu de C.

Sans le mouvement vers l’intérieur le corps couvrirait un arc AC = r·Ω·Δt ≈ HC (Figure 19bis).

 

Figure 19bis : Le calcul de la distance déviée Δs₂.

 

Le calcul infinitésimal nous permet de considérer les arcs AC ≈ HC et FG ≈ EG. Avec la déflexion Δs₂ nous avons EG + Δs₂ = HC, ce qui donne Δs₂ =HC – EG ≈ AC – FG = r·Ω·Δt – (r – Δr)·Ω·Δt = Δr·Ω·Δt = a·Δt²/2, avec a = 2Ω·Δr/Δt = 2Ω·v comme l’accélération dirigée vers la gauche.

 

8. Encore la deuxième loi de Kepler

Enfin, retournons là où on a commencé, avec la dérivation géométrique de la deuxième loi de Kepler, la « loi des aires », ou la conservation du moment angulaire, par Isaac Newton dans les Principia. Noté comme L, le moment angulaire est le produit de la vitesse angulaire R × Ω et de la distance du centre de rotation R

L = R × (R × Ω)

(par unité de masse), où R est la distance au centre de rotation Ω. L et peut souvent être considéré comme scalaire (L), puisque l’axe de rotation et le bras ou le levier sont perpendiculaires l’un à l’autre (comme c’est le cas avec les toupies, les patineurs, les danseurs de ballet et les manèges). Alors,

L = R²Ω

Le moment angulaire est conservé s’il n’y pas de couple, i.e. pas de force agissant dans la direction de rotation. Dans le cas indiqué ci-dessus, il existe en effet une force agissant contre la rotation, c’est-à-dire la force qui crée l’accélération de Coriolis. En donnant l’ordre de grandeur des arcs au moyen de lignes droites, nous pouvons voir que dans la Figure 17 l’aire EGO est plus petite que l’aire HCO, ce qui veut dire que le moment angulaire n’a pas été conservé mais a décru (figure 20).

 

Figure 20 : L’aire couverte par le mouvement vers l’intérieur (triangle rouge) est plus petite que l’aire couverte par le mouvement de rotation qui n’est pas touché (aire verte).

Pourtant, en l’absence de couple, le mouvement continue en direction de D et l’aire couverte par le mouvement s’accroît. En mobilisant le même argument que Newton, nous pouvons prouver sans difficulté que l’aire EDO = l’aire HCO et que le moment angulaire est conservé (figure 20bis).

 

Figure 20bis : La même chose que dans la Figure 20, mais sans couple le moment angulaire est conservé.

 

Dans l’exemple ci-dessus, la vitesse angulaire a augmenté. Ceci s’accorde avec ce que l’on sait d’un danseur de ballet tournant sur place, ou d’un patineur, qui tous deux ramènent leurs bras afin de tourner plus vite. L’accroissement de l’énergie cinétique découle de l’effort musculaire du danseur ou du patineur contre la force centrifuge. Ainsi, même si le moment angulaire est conservé, l’énergie cinétique de rotation ne l’est pas[8].

 

9. La beauté avec les mathématiques

Les Principia de Newton et notamment sa preuve de la deuxième loi de Kepler ont exercé une fascination sur bien des physiciens, dont Richard Feynman (1918-1988), qui parmi d’autres exemples en fait usage dans le chapitre 2 de son livre The Character of Physical Law (Penguin, 1964) pour clarifier la relation des mathématiques à la physique :

Une autre chose, très étrange, qui est intéressante dans la relation des mathématiques à la physique est le fait qu’au moyen d’arguments mathématiques on peut montrer qu’il est possible de commencer d’un de plusieurs points de départ apparemment différents et pourtant arriver à la même chose (p. 50).

Il a ensuite montré que la loi de gravitation pouvait être formulée de trois manières à première vue différentes : en tant que loi de Newton, en tant que méthode de champ local et en tant que « principe minimum » variationnel.

Scientifiquement, elles sont équivalentes... Mais psychologiquement, elles sont très différentes à deux égards. D’abord d’un point de vue philosophique : vous pouvez aimer ou non l’une ou plusieurs d’entr’elles. Ensuite, d’un point de vue psychologique, car elles sont loin d’être équivalentes lorsqu’il s’agit de deviner de nouvelles lois (p. 53).

Il en va de même pour les dérivations mathématiques de l’effet de Coriolis : elles sont différentes mais elles donnent le même résultat. Libre à vous de choisir celle que vous préférez et celle qui à tout moment vous aide à tirer de nouvelles conclusions ou même, pour citer Feynman, à « deviner des lois nouvelles ».

 

 

 

 

(juillet 2017)

 

(traduit de l’anglais par Helen Tomlinson)